FSI

A fast selected inversion algorithm.

Description

Consider a normalized block p-cyclic matrix

\begin{equation} \label{eq:M} M = \begin{bmatrix} I & & & B_1 \\ -B_2 & I & & \\ & \ddots & \ddots & \\ & & -B_L & I \\ \end{bmatrix}, \end{equation}

FSI computes a selected inversion of \(G = M^{-1}\).
The selected inversion is a collection of selected blocks of \(G\). For example, given two integers \(c\) (\(L\%c = 0\)) and \(q\in[0,c-1]\), FSI computes \(L/c\) selected block columns
\begin{equation}\label{eq:S} \mathcal{S} = \{G_{k\ell}\, |\, 1 \leq k \leq L \,\, \mbox{and} \,\, \ell \in \mathcal{I}\} \end{equation}

where \(\mathcal{I} = \{ c-q,\, 2c-q,\, \ldots,\, (L/c)c-q\}\).

(The selected inversion is not limited to block columns. For more patterns please see the Reference [1].)
FSI algorithm consists of three steps:
1. Clustering: block cyclic reduction (BCR);
2. Inversion: block structured orthogonal factorization and inversion (BSOFI);
3. Wrapping: seeds + adjacency relations \(\rightarrow\) selected inversion.
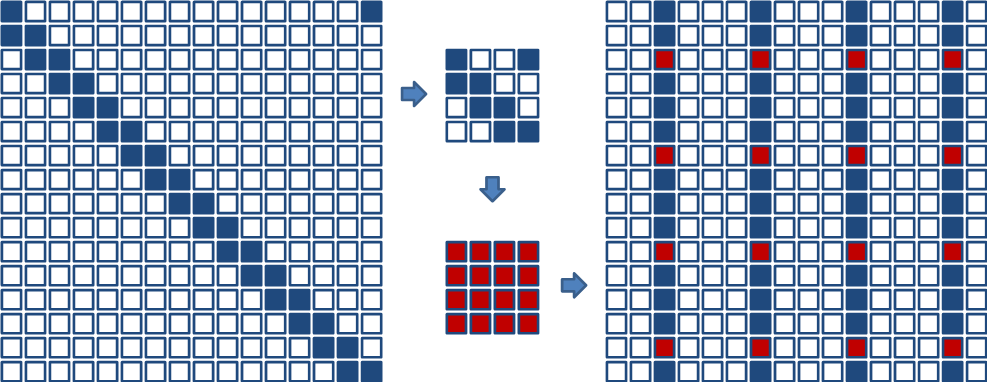
Fig.1: Graphical illustration of the three stages of the FSI algorithm.

Parallel application on computing Green's functions in many-body Quantum Monte Carlo Simulations. Details in Ref.[1, 2, 3].

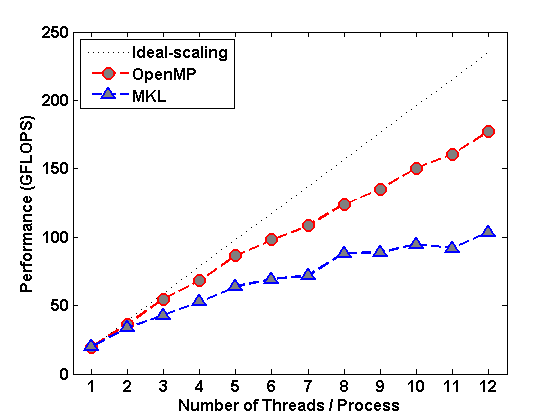
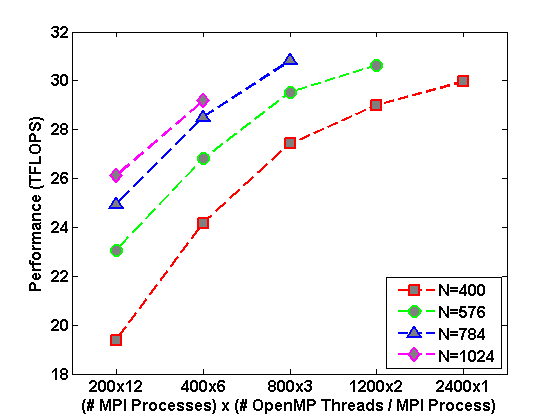
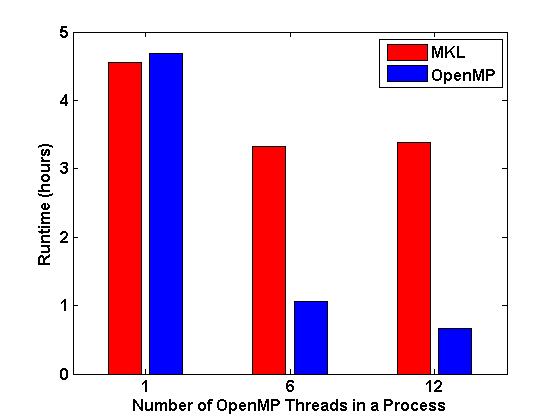
Fig.2 : Left: FSI Performance with OpenMP; Middle: FSI Performance with OpenMP/MPI; Right: Runtime of DQMC

Chengming Jiang, Zhaojun Bai and Richard Scalettar. A fast selected inversion algorithm for Green's function calculation in many-body quantum Monte Carlo simulations. In Proceedings of the 30th IEEE International Parallel and Distributed Processing Symposium (IPDPS 2016), pp. 473–482, 2016. (preprint)
Talk at International Parallel and Distributed Processing Symposium (IPDPS) 2016. (slides)
Poster at (1) SIAM Conference on Applied Linear Algebra 2015 and (2) Bay Area Scientific Computing Day (BASCD) 2015. (poster)